Perspective and 3-D
As the previous sketch suggests, at one end of every visible ray of light is a light source—but what lies at the other end? If a light ray is indeed to be visible, then eventually, perhaps after some reflections off of intermediate objects and the ground, it must reach the human eye. Thus the position of the viewer acts as an important implicit or explicit parameter in every computer graphic image.
Accommodating the observer's vantage gives rise to the rich topic of geometric perspective, in which a three-dimensional scene (defined in space) is transformed into a two-dimensional image representing the view of that scene from a particular position (the viewer's or camera's position). Perspective and other projective functions open the door to 3-D computer graphics, as each possible viewing position corresponds to a unique two-dimensional view of the invariant three-dimensional scene. In computer graphics applications, the scene is an abstract geometric model, the view is the two-dimensional computer screen, and the projective transformation, which maps one to the other, is the work of modeling software or hardware.
While developing the mathematics behind projective transformations is beyond the scope of this paper, suffice it to say that there are many possible geometric flavors of projection, each meeting different requirements of various visualization tasks. In traditional perspective projection, "foreshortening" causes objects in the distance to appear smaller than objects close at hand. While offering a convincing two-dimensional view of a three-dimensional object, perspective's tendency to shorten some distances and not others makes it difficult to take accurate measurements directly from a perspective drawing. Thus engineers usually prefer to employ a parallel or isometric projection in their computer-generated drawings. Similarly, though perspective projections offered a degree of realism considered attractive by European painters in the fifteenth and sixteenth centuries (in whose paintings every foyer's floor is beautifully tiled, to demonstrate the perfection of the artist's perspective), rigid geometric perspective has not always been considered beautiful. Centuries earlier, Chinese landscape artists developed a projection system in which distance into the scene was represented simply by height in the view of that scene. In this system, a painting of a village might depict two houses (one more distant than the other) as one atop the other, where Western geometric perspective would portray one as smaller than the other.
Beyond describing flat, foreshortened images that look somewhat three-dimensional, geometric perspective can be used in computer graphics to create scenes that seem to have genuine depth. Our depth perception comes from our binocular vision: our eyes are physically separate, so each eye sees a slightly different perspective on a three-dimensional scene. The brain fuses these two horizontally disparate images into a single scene enhanced by depth. By creating two images of a single scene taken from slightly different camera positions, and then projecting each image separately onto each of our eyes, computers can stimulate our natural tendency to merge disparate two-dimensional images into unified, three-dimensional scenes.
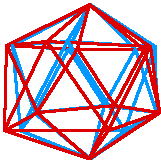 |
Figure 8: Stereo Icosahedron |
Figure 8, from a sketch by Bill Finzer, superimposes two perspective images of an icosahedron. On a computer screen, each image is colored separately. When viewed through stereo glasses (which filter out a different color from each eye's view), the icosahedron seems to float in space. The appearance of three dimensions is quite convincing, even though the construction is entirely two-dimensional. Because the perspective difference between images is determined by a geometric model of the distance between one's eyes, viewers of the sketch in Sketchpad can alter the projection to suit the stereo-optics of their own anatomy—or, by greatly changing the horizontal disparity, the anatomy of a hamster or a rhinoceros!