Fractal Foliage
(BROC1.GSS)
Note that this is a script file to be used with version 3 of Sketchpad. It will not work with version 4.
While the morphing construction suggests the expressivity of some graphics techniques, it also demonstrates a central weakness of many. For a morph to be effective or realistic, its mapping function needs to be appropriately chosen based on the appearance of the pre-image and image. For complicated images, deriving an appropriate mapping function is no easy task. Morphing is therefore considered expensive, in that it costs geometers time to come up with convincing results. Where cost is an issue, computer graphics designers look for ways to reduce the overall expense of a graphical image.
One such "labor-savoring" technique frequently used in creating photorealistic images is to deploy fractals whenever the desired image includes naturally self-similar elements (such as mountain ranges, forests, and coastlines). Fractals have the economic benefit of expressing an arbitrarily rich amount of detail through a relatively simple geometric description. If a desired computer image is to include a tree with thousands of leaves, a graphics designer's time will be better spent coming up with a single fractal construction describing the shape of the entire tree than spent creating separate geometric models for each individual leaf.
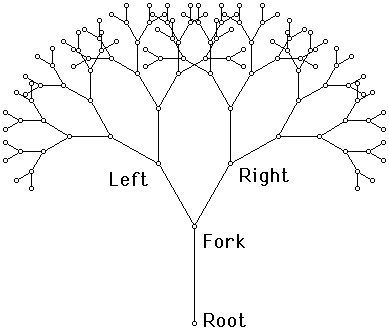
| A favorite and easy fractal to explore in the context of creating naturalistic images is the binary tree, which in its basic shape closely resembles a stalk of broccoli. A binary tree has a central trunk or stalk, which splits in half into two smaller stalks. Each of these splits again, and the ever-smaller stalks themselves split, ad infinitum. You can model a fractal broccoli like the one in Figure 3 with a Sketchpad recursive script: |
Given:
- Point Root
- Point Fork
- Let Trunk = Segment between Point Fork and Point Root.
- Let [B'] = Image of Point Fork dilated by 175.00% about center Point Root (hidden).
- Let Right = Image of Point [B'] rotated -30.0° about center Point Fork.
- Let Left = Image of Point [B'] rotated 30.0° degrees about center Point Fork.
- Let [k] = Segment between Point Left and Point Fork.
- Let [l] = Segment between Point Right and Point Fork.
- Recurse on Fork and Left.
- Recurse on Fork and Right.
Further Exploration
Beyond the suggestions listed here, [Peitgen] is a rich source of activities exploring fractal shape and dimension.- Figure 3 shows a binary tree with a "recursive depth" of five: beyond the first fork, there are five smaller forks in every direction. How many forks are there in the entire tree? How many forks would there be in a tree with a recursive depth of eight? Of n?
- Assume that the main trunk of the tree is one unit long. In a tree of depth 5, how long would all the trunks be, in units, if you laid them end to end? In a tree of depth n?
- Again assuming that the main trunk is one unit long, how tall is the tree at depth five? At depth six? Is there a limit to how tall the tree can grow?
- Though pretty, Figure 3 isn't a very useful Sketchpad illustration, because dragging parts of it changes only the overall scale of the tree. That's because the relative length of each trunk to the trunk from which it grew is fixed in the script (at 75%), and the branching angle between forks is also constant (60°). See if you can create a fractal script that requires as given an adjustable angle ABC and an adjustable ratio j/k in addition to points Root and Fork. Grow a tree using this angle as the branching angle, and using the adjustable ratio to determine the size of each trunk in relation to the trunk from which it grew. Then change the angle and ratio dynamically, to experiment with a family of fractals like the ones shown in Figure 4.
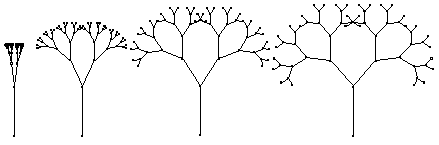 |
Figure 4. A Dynamic Broccoli Forest |