Advanced Sketch Gallery
The Advanced Sketch Gallery is a collection of sketches featuring advanced mathematical concepts, custom tools, and striking visualizations, created by Sketchpad users around the world. They are arranged loosely by topic:
Contents [hide/show]
The sketches are all available for dowload for your personal or classroom use, but are copyrighted by their authors; please contact the author of a sketch if you are interested in using it in other contexts.
If you have trouble downloading Sketchpad documents from your browser, you may need to configure your browser.
Toolkits
Toolkit documents contain collections of related custom tools you may find useful in your own explorations.
|
Graphing ToolkitThis set of tools and accompanying Instructional Manual (16 page PDF file) add many capabilities of advanced graphing calculators to Sketchpad, including finding roots, plotting tangents, and calculating integrals. Bjørn Felsager, 2004 Download: Graphing_Toolkit.gsp |
|
|
|
|
Boolean ToolsThis sketch provides a set of Boolean operators, comparison tools, and Boolean functions, as well as detailed explanations of how these tools were created and how you can make them for yourself. Scott Steketee, 2005 Download: Boolean.gsp |
3D Explorations
Although Sketchpad's native domain is the geometry of the plane rather than the geometry of space, many sketches construct the projection of higher-dimensional mathematical models onto the two dimensions of the computer screen.
|
|
|
3D ToolkitsCheck out the custom toolkits for developing 3D sketches available in the Toolkits section as well: 3D Plotting Toolkit; 3D Invisibility Toolkit. |
Beyond Euclid
Sketchpad is based largely on a Euclidean view of geometry. However, it is possible to both model other geometries within Euclidean geometry, and to use non-Euclidean capabilities in Sketchpad (such as the Calculator) to explore alternate geometries within Sketchpad. This section offers some examples.
Minkowskian GeometryThis sketch and extensive documentation provide an introduction to the Minkowski geometry, instructions for creating constructions with the sketch provided, and notes for presenting a two-part Sketchpad workshop introducing Minkwoskian geometry. Bjørn Felsager, 2004 |
Poincaré Disk Model of Hyperbolic GeometryThis sketch from Sketchpad's Samples collection depicts the hyperbolic plane using the Poincaré Disk model, in which a line through two points is defined as the Euclidean arc passing through the points and perpendicular to the circle. Custom tools allow you to create constructions in the hyperbolic plane. Sketchpad Samples Download: Poincare_Disk.gsp |
Elliptical/Spherical ToolkitTools for exploring elliptical geometry, in which the Euclidean plane is replaced by the surface of a sphere, and lines in the plane are replaced by great circles on the sphere. Brad Findell, 2004 Download: Elliptic_Spherical_Toolkit.gsp |
Euler's Formula and the Complex PlaneA walk-through of the geometric interpretation of one of Euler's most famous results:Nick Jackiw, 2003 Download: Euler's_Formula.gsp |
Half Plane Model of Hyperbolic GeometryTools for constructing in the half-plane model of hyperbolic geometry, in which only points on one side of a horizontal boundary line are considered. A "line" through two points in this model is a semicircle whose center is on the boundary line. Tools for exploring isometries and triangle centers in this model are also included. Judit Abardia Bochaca, 2004; Dan Bennett, 2001 |
Machines and Mechanisms
Sketchpad provides an excellent medium for prototyping, visualizing, and demonstrating "mathematical machinery" of all forms. These sketches contain some ambitious mechanical constructions.
Animated BillboardThis sketch simulates a changing billboard sign. The sign is made of vertical louvers, each of which is a triangular prism. By synchronizing the rotation of the louvers, three different sign faces alternate on the same billboard. The sketch includes a toolkit for making your own billboards, and extensive notes on the design and implementation of the simulation's sophisticated "conditional construction." Paul Kunkel, 2007 Download: Billboard.gsp |
This anthology collects several famous mechanical linkages—Peaucellier cell, a windshield wiper, and a sewing machine needle—in demonstrations both of their outer kinematics and their inner structure. An additional sketch on cam couplings allows you to design your own cam, either by cam shape or by desired rotary profile. |
Other Explorations
These sketches illustrate other unusual or advanced topics in Sketchpad.
|
Statistics Collection
Bill Finzer, 1993/2003 |
|
|
|
This sketch constructs the first 360 Kimberling triangle centers of a single reference triangle, including its centroid, incenter, circumcenter, orthocenter—and several hundred more. Each center includes Kimberling index and barycentric coordinate equations. |
|
 Knot Toolkit
Knot Toolkit Piecewise Function Toolkit
Piecewise Function Toolkit 3D Plotting Toolkit
3D Plotting Toolkit 3D Invisibility Toolkit
3D Invisibility Toolkit Advanced Tools
Advanced Tools Conic Connections
Conic Connections 3D Gallery
3D Gallery Icosahedron
Icosahedron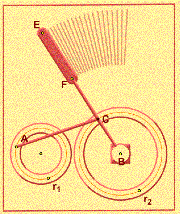 Linkage Library
Linkage Library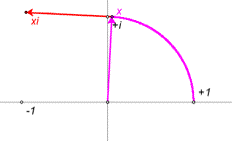 Euler's Formula and the Complex Plane
Euler's Formula and the Complex Plane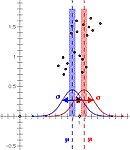 This set of statistics visualizations and questions includes sketches of mean, least squares, r squared, the normal curve, comparing two means, and chi square.
This set of statistics visualizations and questions includes sketches of mean, least squares, r squared, the normal curve, comparing two means, and chi square.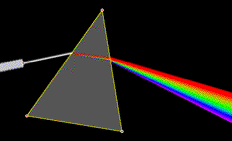 Rainbow Investigation
Rainbow Investigation Dynamical Systems
Dynamical Systems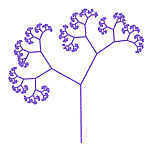 Fractal Gallery
Fractal Gallery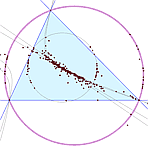 360 Triangle Centers
360 Triangle Centers Penrose Deflation
Penrose Deflation