Activities from the Joint Mathematics Meeting 2006

San Antonio, Texas
January 2006

The Sketchpad User Group had its first meeting of 2006 at the Joint Mathematics Meetings of the American Mathematical Society and the Mathematical Association of America in San Antonio. This page collects the activities and sketches that several participants shared with their colleagues at the User Group meeting. You can download these documents individually, or as a complete collection in a .zip archive or a .sit archive. You are free to use these materials for your personal exploration and for use with your own classes, and to duplicate them for those purposes.

These sketches require Sketchpad 4.0 or later. Many of these documents contain multiple pages. If you have difficulty downloading these sketches individually by clicking on them, consider downloading the entire collection, or right-click (Windows) or Ctrl+click (Mac) their links and choose Download Link To Disk or its equivalent. For more information, read about configuring your Web browser.

Keynote Presentation: Conic Sections in Classical and Taxicab Geometry

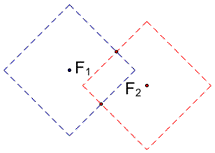Presenter: William Fenton, Bellarmine University and Sr. Barbara Reynolds, Cardinal Stritch University

The featured session at the Sketchpad User Group this year was an introduction to taxicab geometry. The presentation highlighted how our assumptions about how distance is measured effect the shape of space; we looked at conic sections constructed using both the Euclidean metric and the taxicab metric. The material comes from Chapter 5 of College Geometry Using The Geometer's Sketchpad.

Download Presentation Sketch

It's One Thing to Construct, and Another Thing to Explain

Presenter: Jeff Barrett, Illinois State University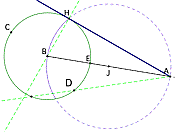

Presentation Description: This presentation discusses the use of a sequence of related sketches as a tool for conveying an explanatory proof through motion sequences and images. The presentation will address the construction of a tangent to a circle through an external point, and share ways to use sequences of sketches to capture a story line to an explanatory sequence of ideas. This was done as a conclusive lesson following students' own efforts to explain the construction. While students could construct such a tangent, they were surprised by the explanation involving a limiting sequence of points along a circle.

Presentation Materials: sketch, handout

Explorations in Transformational Geometry

Presenter: William Fenton, Bellarmine University

Presentation Description: This demonstration engages participants in a discussion of transformations in the Euclidean plane, using Sketchpad. The material comes from Chapter 6 of College Geometry Using The Geometer's Sketchpad, from Key College Publishing.

Presentation Materials: sketch, handout

Geometry of the Earth and Universe Labs

Presenter: Sarah J. Greenwald, Appalachian State University

Presentation Description: A segment on the geometry of the earth and universe stretches the imagination while developing visualization skills and highlights real-world applications of geometry and connections to art, philosophy, physics, astronomy, and geography. This segment can be aimed at students with no math background, at graduate students in geometry and topology, or at any level student in between. We will explore a series of Sketchpad activities on Euclidean and non-Euclidean geometry and discuss how they can be incorporated into a Shape of the Universe segment. Mathematics of the Cosmos was the 2005 Mathematics Awareness Month theme.

Presentation Materials: sketch, handout

Sums of Sinusoidal Functions

Presenter: Molly Jones, KCP Technologies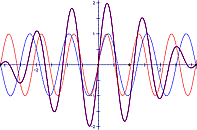

Presentation Description: Using an activity from Exploring Precalculus with The Geometer's Sketchpad as our starting point, we examine sinusoidal functions. In particular, we investigate the behavior of the sum function of two sinusoidal functions. We look at wave packets and simulate wave motion. Finally, we play with a model of sound wave superposition in a piano.

Presentation Materials: sketch, handout

Solving General Triangles

Presenter: Michael Mays, West Virginia University

Presentation Description: This laboratory is used in a trigonometry course at WVU. The goal is to build a geometric intuition about solutions to general triangles. The analytic approach is to work with the Law of Sines or the Law of Cosines directly, but Dynamic Geometry allows us to determine solutions by manipulating geometric objects (line segments and angles) directly. This activity is easy to distribute either as a Sketchpad file or as JavaSketchpad applets.

Presentation Materials: sketch, handout

Explorations of the Hyperbolic Plane

Presenter: Sr. Barbara Reynolds, Cardinal Stritch University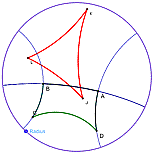

Presentation Description: This demonstration engages participants in a discussion of properties of the hyperbolic plane using the Poincaré Disk tools that come with Sketchpad. This material comes from Chapter 9 of College Geometry Using The Geometer's Sketchpad, from Key College Publishing.

Presentation Materials: sketch, handout

Exploring the Parallelogram via Symmetries

Presenter: Walter Whiteley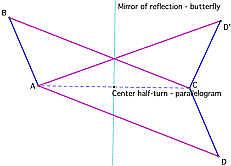

Presentation Description: In practice, almost all proofs of properties of parallelograms rely on a congruence—the half-turn symmetry. We explore this definition of a parallelogram as a quadrilateral with a half-turn symmetry. We see how this symmetry gives easy access to all of the properties, and how most alternative proofs/definitions use this symmetry as the core congruence. We also provide a number of extensions to other settings (e.g., the sphere, 3-space) and to other classes of quadrilaterals. A key point is the role of symmetry in providing a mathematical basis for extensive reasoning with Sketchpad, with physical objects (provided), and with mental processes.

Presentation Materials: sketch, activities handout, instructor notes handout