Building Microworlds for Complex Numbers
Fortunately, these laborious constructions can be abstracted into new fundamental tools within the software. Beyond geometric operations and mathematical definitions, dynamic geometry software has, since its first conception, offered sophisticated facilities for virtualizing composite constructions into new conceptual units, that can then be applied atomically as "extended primitives" of the software. This idea is found in Sketchpad scripts and custom tools, or in Cabri macros. It reflects a deeper tradition stemming from earlier didactic geometry technologies, including the "Repeat" mechanism of The Geometric Supposer software of the mid-1980s, and of course the idea of subroutines in Logo and other programming languages. Among other things, these technologies permit a teacher or curriculum developer to provide a pre-made dynamic geometry environment that has been extended to include tools for a particular topic or area of investigation[1]. We use them here to develop basic microworlds for complex arithmetic and function visualization.
In version 4 of Sketchpad, such extensions take the form of custom tools, devices that define new objects (much as a compass or straightedge defines new objects) and that appear—after they have been created—in the software's basic toolbox along with its fundamental tools (such as the electronic compass and straightedge). The most straightforward way to define such a custom tool is by example: having built an appropriate construction within the software—such as Figure 1—a user can identify the portion (or totality) of the construction to be repeated, and then to Create A New Tool. Sketchpad responds by abstracting the operation away from its particular geometric (or coordinatized) form, and then summarizing it as a symbolic procedure. This procedure describes the function of a new tool added to the toolbox. Custom tools may be simple or sophisticated, and may draw on geometric constructions, planar transformations, or arithmetical or algebraic derivations to define the objects they produce. Figure 2 shows the procedural view of two equivalent custom tools that provide definitions of complex addition, one based on geometric translation, the other based on coordinate arithmetic.
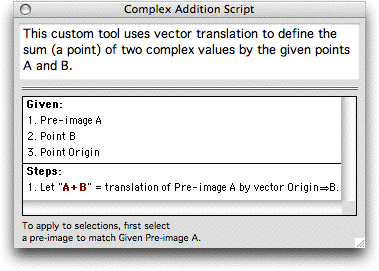

Figure 2. Two addition tools, with separate
derivations but equivalent results.
While such verbal descriptions of a custom tool's procedure can be inspected, or edited, by users, once the tool has been defined, there is no requirement that the verbal procedure ever be referenced again. Instead, users can choose the tools by name from the main toolbox, and wield them directly in the sketch. (In the case of the tools in Figure 2, clicking a "Complex Addition" tool on any two points will produce a third point, their sum.)
Figure 3 shows a toolbox of basic complex arithmetic tools, as well as two notational tools.[2] (Clicking the Cartesian or Standard value tools on a geometric point produces a textual notation of its complex value, in one of the two notations illustrated in Figure 4.) | 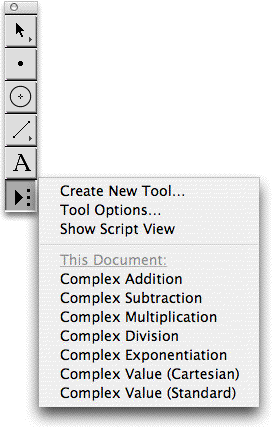 Figure 3. Custom toolbox for |
The benefit of having a coherent toolbox of related tools present at the start of a student investigation or activity, rather than only as the object or endpoint of an activity, is dual. First, clearly, the focus and content of that activity can be on the behavior or properties of the phenomena being modeled by those tools, rather than on the mathematics of the modeling act. Second, since these tools encapsulate mathematical constructions that are at times themselves sophisticated, students combining them can work at a much higher level of mathematical sophistication without requiring a correspondingly much higher level of technical sophistication (with the software) or conceptual sophistication (with the entire network of relationships from which the higher-level construction's behavior emerges from the combined effect of the behavior of each of its components' procedural subconstructions).
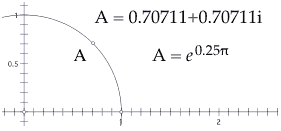
Figure 4. A complex value (point A, left) described in
Cartesian (upper) and Standard (lower) notation.
As students work, they can extend the toolbox with additional tools that they themselves find useful—and that, presumably, they themselves create. This process may repeat itself at several layers of abstraction over the course of an activity or an exploration, as students apply existing tools to define new ones at progressive levels of sophistication or abstraction.
---