Dynamic Geometry and Complex Numbers

A great leap forward in the history and development of the complex numbers comes some 250 years after Cardano first proposes them, in the near-simultaneous realizations of Argand, Gauss, and Wessel that a complex number can be interpreted as, and represented by, a geometric point in two dimensions. This simple correspondence introduces not only the ability to visualize the complex numbers—or, now, the complex plane—in a simple and straightforward sense, but to bring geometric techniques to the interpretation and analysis of the mathematics of that complex plane. With this deft movement, the connotation of the imagination in "imaginary numbers" shifts quickly from imagining their gross mathematical absurdity to imagining their great mathematical potential.

Over the past decade, interactive geometry software environments such as The Geometer's Sketchpad (Jackiw, 1991) and Cabri Geometry II (Laborde & Bellemain, 1992) have rapidly come to play large roles in contemporary planar geometric visualization and exploration, both within school and undergraduate education, but also—though to a lesser degree—within mathematical research. This paper's purpose is to explore the potential for using these software tools to investigate and model complex numbers and their operations, and to visualize functions defined on the complex plane.

Of course, the present work is not the first Dynamic Geometry perspective on complex numbers. One of the activities to which software tools like Sketchpad were first applied in the early 1990s was geometric modeling, and thus the geometric interpretation of complex values was quickly explored by early enthusiasts of the tools. (Lee Dickey with Cabri, and John Olive, Susan Addington and David Dennis with Sketchpad, are among the early pioneers of such investigations.) Since the fundamental workspace of Sketchpad or Cabri is (an electronic simulation of) the unbounded geometric plane, these programs at their debut in some sense already offered effective models of the complex numbers.

What the tools lack at their most basic level, however, are pre-defined operations on complex values—complex arithmetic, in other words, and perhaps complex integration and differentiation. But within the constructionist paradigm of dynamic geometry software, these were fit operations to be defined by an inquisitive user, who might then not only build models of complex expressions, but models of the operators used within those expressions.

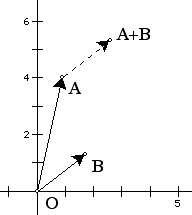Figure 1. Complex addition by vectors.

Thus—for example—the model of complex addition visualized in Figure 1, in which A, B, and A + B are complex numbers, and the dashed vector represents the image of B translated by vector A. Vector addition produces the sum A + B. If the horizontal axis is declared to be real and the vertical axis imaginary, we have computed the complex sum of A and B. Though in the illustration at left, A and B obviously have specific locations and thus fixed complex values, within dynamic geometry software points can be dragged to new locations. Thus dragging A and B generalizes the constructed operation to the addition of any pair of complex numbers.

While such constructions lead to effective demonstrations of the dynamic behavior of basic operations, the act of creating them is not in all cases necessarily revealing to a student first grappling with the ideas of complex arithmetic. The emphasis on such activity is more on the Euclidean operations that must be performed to accurately model a—presumably given—definition of the complex operation, rather than on that operation itself. Such constructions may be a useful exercise in modeling, but they focus more on the model than on the modeled domain.

Previous Page | Next Page