Home > Technical Support > FAQ > Envelope Constructions

FAQ: Envelope Constructions

How do I construct an envelope?

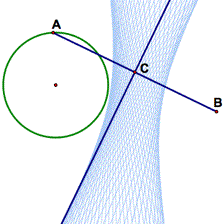A geometric envelope can be thought of as the limit or edge of the locus of a line or a circle. For instance, in the sketch at right, the line through C is the perpendicular bisector AB. The locus of the line as point A travels about a circle clearly suggests a hyperbola. The envelope of the line is the hyperbola itself: the "edge" of the blue locus.

You can construct an arbitrarily accurate approximation of an envelope by constructing the locus of the point of intersection of two arbitrarily closely spaced lines (or circles) in your locus. For this discussion, let's assume (as in the example) that you have a locus of lines determined by the motion of a point A. For each possible position A, think of the corresponding line in the locus as f(A). The envelope of the lines f(A) is the locus of the intersection of f(A) and f(A + delta A) as delta A approaches zero.

Thus, to construct an envelope, you'll need two lines, f(A) and f(A + delta A). You have already constructed the first line f(A)—the line of which you've taken the locus. (In our example, this is the perpendicular bisector through C.) So you need to construct a new line, f(A + delta A), which is "arbitrarily close" to the line determined by A. This means finding a new point, A + delta A, which is arbitrarily close to A, and repeating your construction (of the line determined by A) on this new point (to get the line determined by f(A + delta A)).

How you construct this second point A + delta A depends upon the nature of your locus. In this example, A travels around a circle. So a point "arbitrarily close" to A can be thought of as a point just a little bit farther around the circle than A (for any position of A). On a circle, you can construct this point by rotating A by a small quantity. Drag A to verify that both A and A + delta A move together around the circle.

Once you've constructed the point A + delta A, repeat your original construction using the new point (A + delta A) instead of the old one (A). This will produce a new line, which is likely to be almost parallel to the original line. Intersect the two lines. Then construct the locus of the point of intersection as a function of A's motion around the circle. The result is the envelope.

In this illustration, the distance
between A and A' is 25° instead of 5° for clarity.

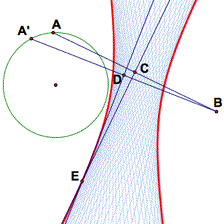Here are step-by-step instructions for the example construction, given a construction that begins with a circle c1, a point on circle A, a segment AB, and a perpendicular bisector to that segment we'll call C.

  1. Mark the center of the circle as the center of rotation. Select point A and rotate it by 5 degrees around the center of the circle to construct point A'.
  2. Draw segment A'B and construct its midpoint D. Construct the perpendicular bisector to A'B (a segment perpendicular to A'B passing through D).
  3. Intersect this perpendicular bisector through D with the original bisector through C.
  4. Call the intersection E. Construct the locus of E as A moves around the circle.

Additional Tips

  • If your locus is of a circle rather than a line, you'll have two points of intersection (between the two circles f(A) and f(A + delta A)) instead of one.
  • If your locus' path is a line instead of a circle, translate (in the direction of the line) rather than rotate by a small quantity in order to locate point A + delta A.
  • Because the two lines f(A) and f(A + delta A) are almost parallel, their point of intersection may well be far off-screen. However, you can count on it being selected immediately after you construct it, even if it's not visible. So you can avoid scrolling in step 6 if you simply shift-select point A and construct your envelope immediately after constructing the point of intersection.
  • Alternatively, rather than rotate by 5 degrees, consider rotating by a marked angle QRS. When you construct A', set QRS to be a "wide angle"—say 45 degrees instead of 5. Construct the point A + delta A in this configuration (i.e., delta A = 45 degrees). Continue through steps 3–6 while using a "wide angle." Then, after you've constructed your envelope in step 6, close angle QRS to be only a degree or two. You may be surprised at how little impact the magnitude of delta A has on the appearance of your envelope.)
  • When you're done, be sure to hide the secondary construction (point A', segment A'B, midpoint D, and the perpendicular bisector through D).