Sketchpad for TI Graphing Calculators: Demonstrations and Examples
This page contains an assortment of sketches demonstrating some of the features of The Geometer's Sketchpad for TI graphing calculators. If you'd like to explore them interactively, download the sketches to your computer, and then use TI-GRAPH LINK to copy them from the computer to your Voyage 200, TI-92 Plus, or TI-89 Titanium. Once they've been copied to a calculator, you can VAR-LINK them from calculator to calculator to share with an entire class.
If you wish to download all six of the sketches, click here for a .zip file. (Once you have unzipped all six files, follow the same steps using TI-GRAPH LINK to copy them to your calculator.) Some browsers will have difficulty copying the single files that appear below. Should you have problems, download the .zip file.
 Danny's Ellipse Danny's EllipseThis construction, based on a sketch by Danny Vizcaino (a student at Monte Vista High School in California), generates an ellipse. But the two foci of the ellipse are not part of the construction! Can you prove that the result is nonetheless an ellipse, and go on to construct its foci? Download: DanV.9xy
|
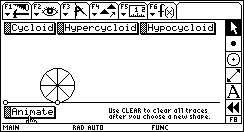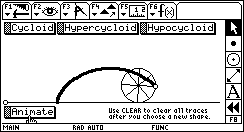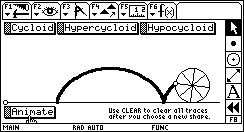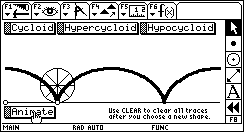 Cycloid CycloidThis sketch traces the path of a point on the circumference of a rolling wheel (a cycloid). Download the sketch to experiment with a point on a spoke of the wheel or a point on the extension of a spoke. Download: CYCLOID.9XY
|
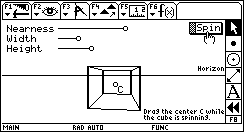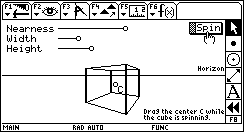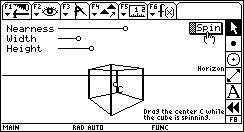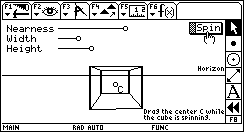 Spin Cube Spin CubeThis sketch rotates a cube in two-point perspective. Dragging the horizon line and changing the controls at the top of the sketch allow you to alter the projection of the cube. (Use commands in the F2 menu to alter the speed of rotation.) Download: SPINCUBE.9XY
|
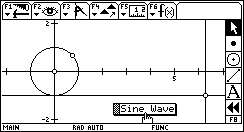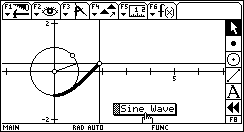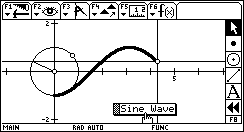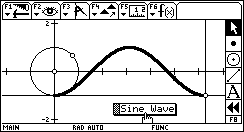 Sine Wave Sine WaveThe sine of an angle can be visualized in the height of a point moving about the unit circle. This sketch intersects a horizontal line through that point with a vertical line moving left-to-right to plot a sine wave. How far along the x-axis should the vertical move to complete one complete phase of the sine wave? Download: SINE.9XY
|
 Ellipse EllipseThis sketch demonstrates a more traditional approach to an ellipse construction than Danny's Ellipse (above). As C moves between A and B, the sum of the distances AC + CB remains constant. The two circles have centers f1 and f2, and radii AC and CB. Thus, the intersections of these circles trace the set of points, the sum of whose distances from two points (f1 and f 2) is constant (AC + CB, or AB). Download: ELLIPSE1.9XY
|
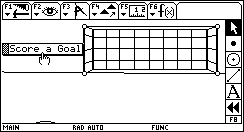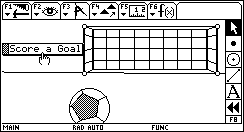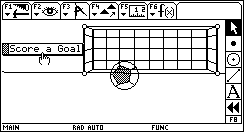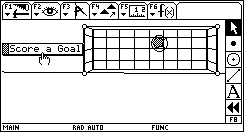 GOOOOOAL!!! GOOOOOAL!!!This sketch—just for fun—uses dilation to visualize a scene in one-point perspective. Download: Goal.9xy
|
 Equilateral Triangle Equilateral TriangleProposition 1 from the First Book of Euclid's Elements. Two circles based on a common segment have equal radii. Therefore, the three edges of the triangle have the same length: The triangle is equilateral. This one is so "elementary" its construction is left as an exercise for the reader! |
 Danny's Ellipse
Danny's Ellipse Cycloid
Cycloid Spin Cube
Spin Cube Sine Wave
Sine Wave Ellipse
Ellipse GOOOOOAL!!!
GOOOOOAL!!! Equilateral Triangle
Equilateral Triangle