Discrete Mathematics and Dynamic Geometry

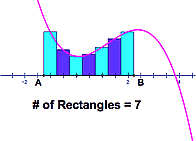
First we start with some examples from opposite ends of the curriculum in which mathematical continuity informs our understanding of discrete phenomena and in which discretized arguments helps build our understanding of continuity. In a circle model of equivalent fractions, increasing the number of smaller parts, part by part, without limit rapidly demonstrates that there is no upper limit to the number of fractions equivalent to a given fraction. Similarly, in integration, we first establish insight into how well or poorly a single rectangle approximates the area over some interval under a curve. The insight that "thin" rectangles fit better than "thick" ones motivates subdividing the interval into two rectangles, then three, and more, with the (discrete) Riemann sum emerging as a powerful model of the (in the limit, continuous) definite integral.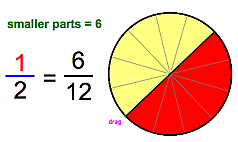

Returning to primary school mathematics, we next look at how by skip-counting numbers on a number chart we can picture multiples of that number or of other numbers we choose. Resizing the chart exposes other important patterns: if we expand the width of a two-multiple chart so that all of the bicolored numbers line up on the right, these are the common multiples, with the first row showing the least common multiple. 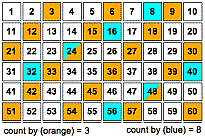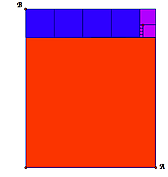In another technique, if we erase 1 and then start repeatedly coloring off all multiples of the least uncolored number left on the chart, we recreate Eratosthenes’ "sieve" of prime numbers.

Moving from the least common multiple to the greatest common divisor, we compare the standard school method of enumerating common divisors to Eratosthenes' sieve and discover: it's even worse! A far more efficient algorithm is found in Euclid's elements, which—among other things—implies it has a geometric form worth considering. Euclid's method recursively remainders two whole numbers until one fully divides the other; this is the GCD. In the geometric form, maximal squares are repeatedly removed from a starting rectangle until the remainder itself is square; this square's edge length gives the GCD (or, geometrically, the largest commensurable measure). Of course, while two whole numbers always have a common divisor (trivially: 1), there is no guarantee that two geometric lengths are commensurable, and thus in the geometric context Euclid's algorithm also gives us a startling picture of irrationality in a never-ending sequence of ever-small squares.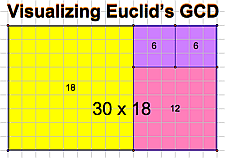

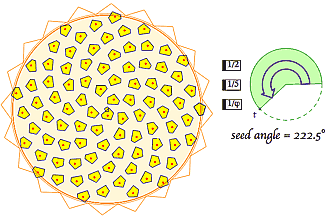
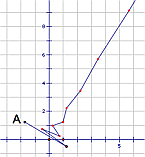
Analyzing the previous configuration for the rectangle that reduces the fastest without ever terminating leads one directly the golden rectangle and to that "most" irrational number, phi. We rederive phi as the ratio, in the limit, of pairs of terms in the Fibonacci sequence, which we model with a recurrence relation first on {1, 1, 2, 3 ... } but eventually with any starting pair of numbers {F[1], F[2], ...}. Plotting and adjoining successive pairs of terms as points (F[n], F[n + 1]) demonstrates slope convergence toward phi. To wrap up, we move from length to angle, and visit the Fibonacci sequence and golden section in the turning angle of seed packings in a growing flower head.

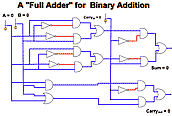
In the final section of the talk, step functions are introduced as a means of transforming the continuum of the real numbers into discretized and eventually finite categorical functions. We explore the prospects for imputing a "logic" onto the infinite integer results of rounding; onto the three-valued categorical defined as the sign (or signum) function; and onto the two-valued categorical that can be easily derived from sign. We pursue the two-valued system—the "simplest" discrete system possible, the "smallest" logic capable of expressing difference or change—into the realm of Boolean algebra, and build simulated logic gates for performing logical arithmetic. Wiring these together in sufficient quantity lets us rederive numeric arithmetic—first in binary, then in decimal—and eventually leads us back "up" to computers and computer programs, like Sketchpad, which through Dynamic Geometry simulate mathematical continuity and the real numbers!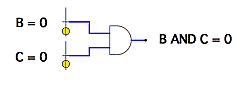