Studies in Light

During the early 1980s, as the field of computer graphics matured, many practitioners moved beyond issues of simple geometric shape and began addressing the more fundamental issue of light as well. It is light's interaction with shape, after all, that gives rise to vision, and in photorealistic images or scenes, the physics of light and the geometry of vision determine the scene's overall composition, coloration, luminance, and shadows. This section looks at a few models of light and vision drawn from perspective and optics.

Nathan's Windmill

Figure 5: Nathan's Windmill

Nathan Reed, a student at Freedom High School in Morganton, North Carolina, submitted Figure 5's sketch in response to a classroom art project. Once animated in Sketchpad, the illustration depicts an austere desert landscape, with the windmill's propellers turning sluggishly in the torrid air. A hot sun travels slowly across the sky. Though a minor detail in the overall composition of the scene (which also contains elements not shown in Figure 5), much of the ambiance of Nathan's "movie" is conveyed by the slow and lengthening march of the shadow cast by the road sign on the empty highway:
Figure 6: Shadowfall on Nathan's Highway (dawn through mid-afternoon)
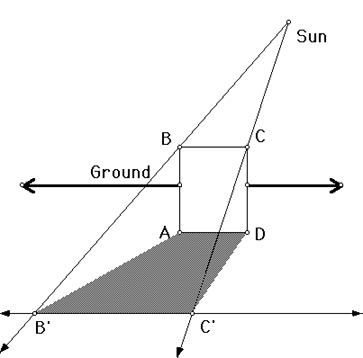Nathan accomplishes the shadow effect by a simple geometric construction which imagines the sun as a point light source, from which rays of light project in all directions. Where the rays pass beyond the edges of the highway sign, light travels freely to the ground, but where the rays are blocked by the interior of the sign, the ground lies in shadow. Thus a ray from the sun which passes exactly through a corner of the sign will eventually hit the ground at the corresponding corner of the sign's shadow.

Figure 7: Shadowcasting, simplified

Figure 7 reduces Nathan's construction to its essential components. Light rays cast from a light source (point Sun) intersect some monolithic object in the scene at its corners (B and C). Thus the shadowed projections of these points must lie along the extensions of these rays (B' and C'). Connecting these corners with the portions of the object which sit on the ground (and therefore touch their shadow: A and D) defines the perimeter of the entire object's shadow. Relocating Sun in the sketch moves the shadow appropriately.

As an accurate model of the physics of such a situation, Nathan's construction is not without limitations. Our own sun, for instance, is sufficiently far away, and planet Earth so small in comparison, that the sun's light rays are effectively parallel. Perhaps Nathan's world has a much smaller, closer sun, however, which acts more like a spotlight than as a general source of diffuse illumination.

More gravely, though, this geometric construction lacks any interpretation of how far behind the monolith ABCD the sun stands. Shadows exist in three-dimensional configurations of objects, light sources, and ground, but this is fundamentally a two-dimensional construction. Thus, the "height" of the shadow—measured as the vertical distance from AD to B' or C'—is arbitrary, rather than determined by the geometry of the scene. In Nathan's example, this height is fixed (as can be seen in Figure 6), where in a more realistic scene, it would vary with the height of the sun in the sky.

These limitations do not detract from Nathan's accomplishment, however. In fact, by choosing to approximate the geometric behavior of a complicated dynamic construction with that of a much simpler one, Nathan adopted a strategy common to computer graphics' practitioners: only devote as many resources to a modeling task as required to obtain the desired degree of realism. Again, where cost is a central issue—here "cost" being the amount of time Nathan had to complete his geometry assignment—figuring out ways to minimize it becomes a creative part of the problem-solving process.

Further Exploration

  • Add a second sun to Figure 7, as might be found in a binary star system. Cast a second shadow or set of shadows. Animate the two suns along different paths through the sky.
  • Experiment with shadows cast by more complicated objects than simple quadrilaterals (like Nathan's highway sign or Figure 7's monolith ABCD). Can you model the shadows cast by an object with non-vertical sides, or by an object with a hole in it?
  • Create a model of light projection similar to Figure 7's, but in which the sun is infinitely far away, and thus casts rays which are all parallel. How are shadows different from Nathan's in such a model?
  • Describe the components of a more complicated model of shadow casting which accounts for the height of the sun (and therefore the height of shadows) geometrically. Can you create such a model in Sketchpad?

Previous Page | Next Page