Kristin's Ferris Wheel
A novel interpretation of this last question—finding the locus of one body (the moon) as it orbits another orbiting body (the earth as it rotates about the sun)—crossed my desk recently in the following sketch, submitted by Kristin Wallace (a high school classmate of Nathan Reed's).
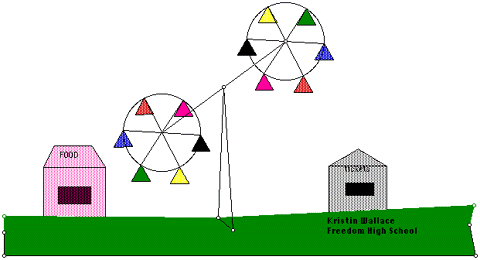 |
Figure 11. The Ferrisferris Wheel |
Figure 11 illustrates a double-Ferris wheel amusement park ride. Two independent wheels rotate on the ends of a structural axis, which in turn spins slowly around its midpoint. Passenger cars hang from brackets mounted at regular intervals along the rotating wheels. Kristin provides an animation button (not shown) that sets the entire contraption in motion.
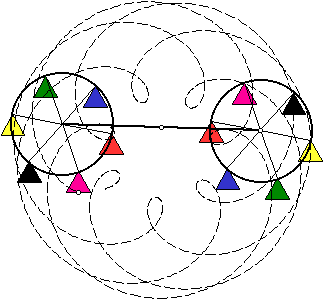 |
Figure 12. The Lunar Orbit |
In terms of the previous astronomical analogy, the midpoint of the axis represents the sun (a fixed "center of the universe"). The endpoints of this axis are two planets orbiting the sun, and the passenger cars are moons of their respective planets, rotating about them as the wheels spin on their hubs. To plot the locus of the moon, simply trace a point on one of the passenger cars while the Ferrisferris wheel spins, as shown in Figure 12.
This complex, many-petaled rose is a form of epicycloid, the curve traced by a point on a circle that rolls on the outside of a fixed circle. That the Ferrisferris wheel requires several revolutions to "close" the curve, as is about to happen in Figure 12, expresses a fundamental relationship between the diameters of the two wheels (one of which is only implicit in the construction), and the number of petals in the rose characterizes the speed of the rolling circle. In terms of a physical interpretation of the epicycloid, multiple petals per revolution implies that the rolling circle is "spinning out" as it drives around the fixed circle. Conversely, if the outer wheel rotated more slowly about its center than around the inner wheel, we'd say it skidded as it rolled.
Modeling amusement park rides with simple geometric graphics can serve a double purpose in the classroom. First, many of these machines—merry-go-rounds, Ferris wheels, Mad Hatter's teacups, and so forth—have motions easily described by a short series of rotations, reflections, and translations. (As far as I know, they've yet to invent an attraction that actually dilates its rider, although with many rides, one frequently feels somewhat dilated on disembarking.) Building geometric models of such mechanisms is an excellent introduction to the basic transformations. Second, passengers on many of these rides trace paths through space that describe classical geometric curves, just as the Ferrisferris wheel provides a physical interpretation of an epicycloid. The tight petals of this curve correspond to the surprising acceleration riders feel (when whipping into retrograde) on such a benevolent-seeming ride!
Another familiar family of curves found in the Ferrisferris wheel can be seen by tracing the height of a rider from the ground over time. To plot this graph in Sketchpad, simply trace the intersection of a horizontal line passing through a single car (representing the rider's height) with a vertical line moving ever to the right (representing time). Figure 13 shows this graph for four different speeds of the spinning wheels. In the first graph, at left, the outer wheel is fixed in relation to the structural axis. This essentially converts the ride into a conventional Ferris wheel, which leads to the smoothest possible motion for the rider. In the second graph, the outer wheel is rotating at the same speed as the structural axis. In the remaining two graphs, the outer wheel travels at twice and three times the rotational speed of the inner axis.
 |
Figure 13. Height of Ferrisferris Car over Time (four different speeds) |
The progression of these graphs is no doubt familiar. Just as the height of a point moving cyclically around a circle projects into a sine wave, the height of a rider on a Ferrisferris wheel—which is composed of two circles—projects two sine waves simultaneously. These graphs simply represent the addition of a large and a small sine wave, where the large sine wave mirrors the constant motion of the rotating structural axis, and the smaller sine wave, which increases in frequency over the graphs' progression, represents the ever-faster travel of the wheel rotating about its hub. The relative amplitudes of the two component sine waves are determined by the relative diameters of the two rotating components of Kristin's sketch. Amusement park rides can thus take us quickly into interesting trigonometry, and beyond to signal analysis: engineers routinely build complex waveforms out of simple sine wave components (to simulate the complex harmonics of a synthesized musical instrument, for example); and conversely, break down complex waveforms into simple sine-wave components (to perform frequency analysis or filtering operations on radio signals, for instance).
Further Exploration
- In Sketchpad, construct a working model of a merry-go-round and a Ferris wheel. Remember that in a merry-go-round, cars (or horses) are fixed, and so the orientation of the center of the merry-go-round is always the same in relation to the rider. (If the merry-go-round travels clockwise, it's always to your right.) But in a Ferris wheel, cars hang freely from the wheel, and so sometimes the center of the wheel is above your head, and other times below your feet. Make sure cars and horses in your models behave appropriately. Are there other geometric differences between the two rides?
- Make a Ferrisferrisferris wheel, in which cars rotate around a second wheel that in turn rotates around a primary wheel rotating on a structural axis. Plot the waveform suggested by the height of a rider in this car over time.
- In a book on physics, signal analysis, or electronic music, look up the definition of a square wave and a saw-tooth wave. How would you modify your Ferrisferrisferris wheel's dimensions to approximate these waveforms?