Building Something that Works
Mathematics in the classroom is too often an end in itself. There must be times when students see math as a tool to be used for some desired goal. "Applications"-type problems frequently postulate some external context in which the mathematics currently under study is useful. Constructivist dynamic manipulation environments offer another, more immediate, context. In them, students can solve problems and address challenges by building interactive, manipulable, mathematical models. Mathematics drives the visual display of these environments, and learners, ourselves included, will go to extraordinary lengths to understand and use math to cause a (simulated) frog's tongue to wiggle just right, a bicycle wheel to turn smoothly, or a Luxo lamp to extend and swivel with properly-constrained mechanical motion. These interactive model-building challenges are often more satisfying than traditional applications problems, because we are not simply told that our solution is physically correct (as we are told that the motion of a projectile follows a parabola), but we can see that it is so. (In such environments, we also quickly visualize the limitations of our models; and frequently go on to improve them in an iterative fashion.)
Example: Symmetry Animations
The model of a frog at right was developed by Alexis McClean (while a student at Mountain Brook Junior High) during an exploration of bilateral symmetry. The frog and flies around it were assembled from compass-and-straightedge constructions which parameterize the orientation of parts of the animals--limbs, wings, eyebrows--through the location of key points (not shown) in the construction. When software is used to animate these points along circular or linear trajectories, the frog fidgets in anticipation as the flies flit about its head. (Press the buttons that Alexis has provided at the bottom of the sketch to launch these points into motion.)
Proposed Standard: Students should have experiences in which they use mathematics to build working, manipulable models with both physical materials and computer tools.
The Behavior of Mathematical Objects
Consider the following two descriptions of an isosceles triangle.
- Two sides are equal in length and the two angles opposite them have equal angle measure.
- No matter how you transform any part of it, the two sides adjust to remain equal in length and the two angles equal in measure.
The first lists two properties of the triangle while the second describes its behavior. The first is declarative and static; the second, imperative and dynamic. The difference is one of emphasis--a particular isosceles triangle representing all isosceles triangles in the first, versus a triangle that can become all isosceles triangles in the second. In learning and problem-solving contexts, the imperative representation of knowledge is richer in generative potential: where a static list of properties lends itself only to recapitulation, a model of dynamic behavior leads to predication and extrapolation. We believe that if you could see inside the minds of mathematics practitioners, you would find imperative, "active" knowledge that models behaviors of objects moving and changing in response to stimuli.
Example: Drag Algebra
Let's take an unlikely example from symbolic algebra. NuCalc is a remarkable algebra and graphing program that has been bundled on over six million Power Macintoshes.
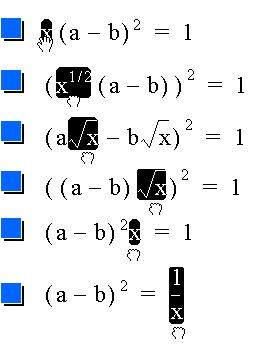 |
In the illustration at left, the user is dragging x from one side of an equation to the other. As x moves inside the squared term, it acquires a square root, which disappears as it moves out again on the right. As x moves across the equals sign, it drops into the denominator. The x has a behavior--or, the equation as a whole has a behavior--in response to the constraint that the two sides remain equal. |
Example: Taylor Series
Consider another example of mathematical behavior, again using NuCalc. The following graph illustrates the function y=sin(x) plotted against the sum of the first n terms of the Taylor series, 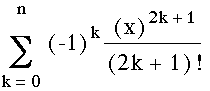 , where n varies from 0 to 4.
, where n varies from 0 to 4.
NuCalc provides a slider with which you can vary the value of n. As you drag the slider, you see the Taylor series plot "flip its tails" and "smooth itself along the sine curve." The opaque algebraic expression becomes a transparent and, eventually, friendly object through graphing and dynamic manipulation.
Proposed Standard: In addition to listing properties of mathematical entities, students should be encouraged to think about and describe their behaviors. Throughout their careers, students should have experience with computer technology that, through dynamic manipulation, encourages this view of mathematics.
Go to the next page, back to the previous page, or to the table of contents.