Newton's Method (Short Version)

Objective

In this activity, you'll use Sketchpad to make use of Newton's method for finding a root of a differentiable function. In the example, you'll use a polynomial function of third degree. This version of the activity uses a prepared sketch and script tool; use the long version if you'd prefer to create the sketch and script tool from scratch.

Steps:

First, you'll construct the graph of a polynomial of third degree.

Step 1: Open the sketch Newton.gsp in the Newton folder. This sketch graphs a third-degree polynomial. You may adjust the sliders to change the coefficients of the polynomial, but make sure you leave the polynomial with three roots. (A root or zero of a function is a place where the function's graph intersects the x-axis.)

Step 2: Set the script tool folder to the Newton folder. To do this, choose Preferences from the Display menu, click the More button, and then click the Set button. Choose the Newton folder in the dialog that appears and click the Select (Mac) or OK (Windows) button. Click Continue in the Advanced Preferences dialog, and OK in the Preferences dialog.

The script tool should appear at the bottom of your toolbox, and "Newton's method" should be one of the tools available when you click and hold the script tool.

Now you'll perform one iteration of Newton's method. Here's a graphical description of Newton's method. First, you choose a starting point on the x-axis, and find the point on the graph that corresponds to the chosen x-value. At this point on the graph, you construct a tangent to the graph. You then find where this tangent intersects the x-axis. This intersection point represents your new x-value, and you begin again.

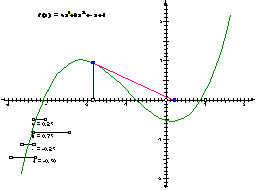
Step 3: Choose the Newton's method script tool, and play it by clicking on a point (the seed point) on the x-axis. The script tool finds the value of the function (represented by the thick blue line) and then at this point traces along the tangent back to the x-axis. The result should look similar to the figure.

Step 4: If the intersection point of the tangent with the x-axis (constructed by the tool in step 3) is too close to an existing point to be distinct, use the Selection Arrow tool to move the seed value so the intersection is distinct.

Step 5: Click the script tool on the intersection point of the tangent with the x-axis. The tool constructs a second iteration.

Step 6: Click the tool again on the intersection point of the new tangent with the x-axis to construct a third iteration. Continue using the tool until you have at least 5 iterations. If the last intersection is not distinct at any stage, adjust the sketch so it is distinct before using the tool again.

Q1. Adjust the seed value so it's fairly close to a root of the polynomial. What can you say about the convergence of Newton's method when the seed is close to a root?

Q2. Move the seed value so it's to the left of the left-most root or to the right of the right-most root. What can you say about the convergence of Newton's method in these situations?

Q3. Adjust your sliders so that the function has three roots. Try some different positions for the seed value between the various roots. What can you say about the stability and convergence of the method under these conditions?

Q4. Adjust your sliders so that the function has only a single root, but also has a minimum or maximum that comes close to the x-axis without touching it. Notice what happens to the iterations as you move the seed value to different positions near this minimum or maximum. What can you conclude about the stability of Newton's method in this situation?

Q5. Can you think of any way of predicting how well Newton's method will do with different seed values, depending on the shape of the graph? Describe your predictions as clearly as you can.

Explore More:

Try this activity with a different function that has several roots. For instance, you could use a sin or cos function. (You will have to figure out how to construct the tangent for each iteration.) What do you discover about the convergence and stability of Newton's method under different conditions on your chosen function?